Uma segunda pessoa procurou encontrar outra maneira…

4 de junho de 202121 de outubro de 2023 admin

(Enem 1998) Observe o que foi feito para colocar bolinhas de gude de 1 cm de diâmetro numa caixa cúbica com 10 cm de aresta.

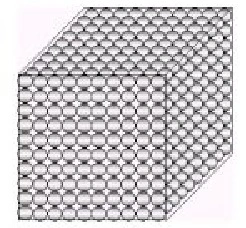
Uma segunda pessoa procurou encontrar outra maneira de arrumar as bolas na caixa achando que seria uma boa ideia organizá-las em camadas alternadas, onde cada bolinha de uma camada se apoiaria em 4 bolinhas da camada inferior, como mostra a figura.

Deste modo, ela conseguiu fazer 12 camadas. Portanto, ela conseguiu colocar na caixa:

a) 729 bolinhas.

b) 984 bolinhas.

c) 1000 bolinhas.

d) 1086 bolinhas.

e) 1200 bolinhas.

Resolução

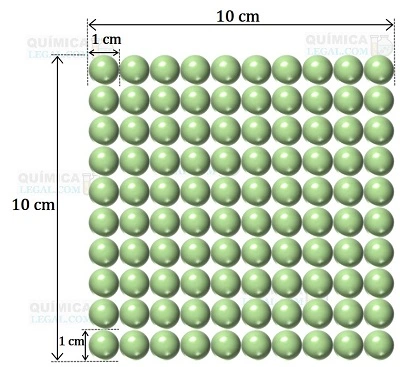
Acomodando 100 bolinhas em sua primeira camada, visto que cada esfera possui um diâmetro de 1 cm e o cubo em questão possui uma aresta de 10 cm, uma representação visual dessa camada pode ser vista na imagem a seguir, capturada a partir de uma perspectiva superior.

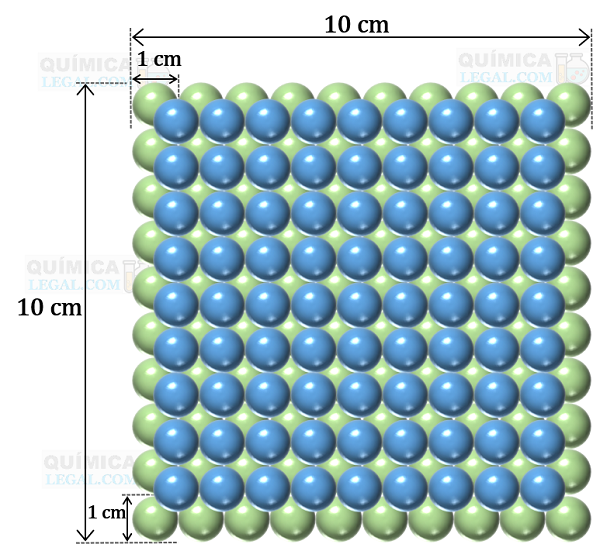
Ao posicionar uma bolinha de gude sobre quatro bolinhas da camada inferior, resulta em uma fileira composta por nove bolinhas, como ilustrado na figura a seguir.

Ao reproduzir a fileira de nove bolinhas, forma-se uma segunda camada que contém 81 bolinhas, equivalendo a nove fileiras, cada uma com nove bolinhas (9×9 = 81), como demonstrado.

Conforme estabelecido no enunciado, conseguimos acomodar 12 camadas de bolinhas na caixa. Dado que essas camadas são organizadas alternadamente, temos 6 camadas com 100 bolinhas e 6 camadas com 81 bolinhas. Portanto, o número total de bolinhas pode ser calculado da seguinte maneira:

Número de bolinhas = (6 * 100) + (6 * 81)
Número de bolinhas = 600 + 486
Número de bolinhas = 1086

Portanto, empregando essa configuração, é viável acomodar um total de 1086 bolinhas no cubo.

Uma questão que frequentemente surge neste exercício é a seguinte: “Como é possível acomodar 12 camadas de bolinhas se o cubo tem uma aresta de 10 cm e cada bolinha tem 1 cm de diâmetro? Não deveriam ser apenas 10 camadas?”

De fato, são 12 camadas. Isso ocorre porque cada bolinha da segunda camada se encaixa entre quatro bolinhas na camada inferior, resultando em um espaço ocupado pelas duas camadas alternadas que é menor do que o espaço ocupado por duas camadas iguais, como ilustrado na figura abaixo.