O retângulo abaixo de dimensões a e b está…

(FUVEST 1992) O retângulo abaixo de dimensões a e b está decomposto em quadrados. Qual o valor da razão a/b?

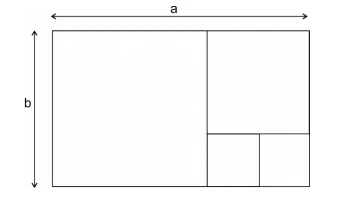
a) 5/3

b) 2/3

c) 2

d) 3/2

e) 1/2

Resolução

Ao numerar os quadrados, atribuímos os números de 1 a 4 da seguinte forma:

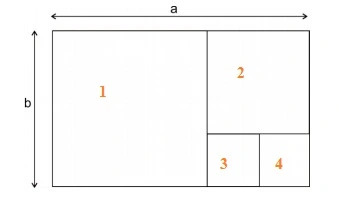
O lado do quadrado 1 pode ser representado como uma função dos lados do quadrado 2 e 3, conforme indicado na seguinte fórmula:

ℓ₁= ℓ₂ + ℓ₃

O lado do quadrado 2, por sua vez, pode ser expresso como uma função dos lados dos quadrados 3 e 4, conforme demosntrado a seguir:

ℓ₂ = ℓ₃ + ℓ₄

Dado que os quadrados 3 e 4 possuem lados idênticos, podemos afirmar que seus lados são equivalentes. Portanto, temos:

ℓ₂ = ℓ₃ + ℓ₃
ℓ₂ = 2 ∙ ℓ₃

Dessa forma, podemos calcular o comprimento do lado do quadrado 1 em termos do lado do quadrado 3, conforme exemplificado abaixo:

ℓ₁= ℓ₂ + ℓ₃ℓ₁= (2 ∙ ℓ₃) + ℓ₃ℓ₁= 3 ∙ ℓ₃

Reexaminando a figura, constatamos que “a” é equivalente à soma dos lados dos quadrados 1 e 2, portanto:

a = ℓ₁ + ℓ₂a = (3 ∙ ℓ₃) + (2 ∙ ℓ₃₎a = 5 ∙ ℓ₃

A medida “b” é, por sua vez, idêntica ao lado do quadrado 1, e, assim:

b = ℓ₁b = 3 ∙ ℓ₃

Por último, resta apenas calcular a relação entre “a” e “b”, ou seja, a razão a/b:

a/b = (5 ∙ ℓ₃) / (3 ∙ ℓ₃)
a/b = 5/3

Assim, podemos concluir que a alternativa com a resposta correta é a letra A.

Gabarito: LETRA A

Confira mais EXERCÍCIOS RESOLVIDOS sobre GEOMETRIA PLANA.